rapidfoki.blogg.se - The artmatic mean

#The artmatic mean plus

Seems too coincidental to not be important, so let’s explore that a bit more. Quantity B, $25$, seems coincidentally placed right smack in the middle between $23$ and $27$. We have one set of numbers with an average of $23$ and a smaller set numbers with an average of $27$. Let’s also pay attention to any coincidental number relationships that we see, since we know to be suspicious of any coincidental number relationships. Let’s start working on a way to estimate this average! If we could estimate the average of the $150$ numbers just to determine if it was equal to $25$, above $25$, or below $25$, we could finish the question. Let’s write that on our paper, with a “?” in between until we figure out which side is greater. Starting with a top-down approach, we know that we want to compare the average of $150$ numbers to the value $25$. Here, our paper is our friend, so let’s put it to good use! So we should always take in all of the numbers and concepts the question presents, then see if anything jumps out at us. However, they can often times have more abstract solutions that require more thought and planning when compared to solutions where we just plug and chug numbers into equations. We know that solving math problems logically can be very rewarding.

#The artmatic mean plus

Challenge accepted! Plus we never know if it might be fun, educational, or both! Develop a Plan and Solve: Logically It might be more challenging to solve this question in a logical way without a calculator. Though we did need to use our calculator at the end, and we know that most problems shouldn’t require a calculator. This is less than Quantity B $(25)$, so the correct answer is B, Quantity B is greater. Since the question asks for averages of sets of numbers, let’s think of the equation we have memorized for averages:

We want to compare the average of all $150$ numbers to the value $25$.

We also have $50$ other numbers with an average of $27$.

We have $100$ numbers with an average of $23$.

Let’s carefully read through the question and make a list of the things that we know. Now that we know what this question likely tests, we’ll be ready for whatever it throws our way! What Do We Know? Whenever we see averages of numbers, we should expect the question to test our Numerical Methods for Describing Data math knowledge. Three times we see the average of different sets of numbers mentioned. Pay attention to any words that sound math-specific and anything special about what the numbers look like, and mark them on your paper. Let’s search the problem for clues as to what it will be testing, as this will help shift our minds to think about what type of math knowledge we’ll use to solve this question. Those questions testing our Numerical Methods for Describing Data knowledge can be kind of tricky, but never fear, PrepScholar has got your back! Survey the Question Buuuut then you had some questions about the quant section-specifically question 6 of Section 4 of Practice Test 1. So, you were trying to be a good test taker and practice for the GRE with PowerPrep online.

The relationship cannot be determined from the information given.

& 4.The average (arithmetic mean) of $100$ measurements is $23$, and the average of $50$ additional measurements is $27$.

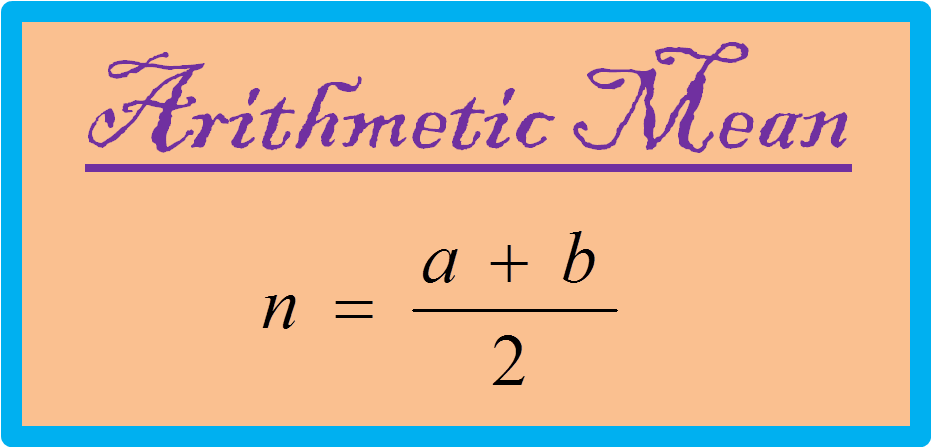
Let X be a discrete random variable with values x 1,x 2,…x n, and probabilities 1/n : This statement can be shown by considering a convex function f(x) = -log x.

Jensen’s inequality, usually taught in a calculus based statistics course, can be used to show that the arithmetic mean of n positive scalars x 1,x 2,…x n, is greater than or equal to their geometric mean, which is equal to Showing the Arithmetic Mean is Greater than the Geometric Mean If the list is a sample, it’s called a sample mean x̄. If your data is a population, then the mean is called a population mean, represented by the letter μ. Solution: The average driving speed is 62.5 mph.įor another example with steps, see the next article:

Step 2: Divide by the number of items in the set. Example problem: Find the arithmetic mean for average driving speed for one car over a 6 hour journey: 54 mph, 57 mph, 58 mph, 66 mph, 69 mph, 71 mph